Après une étude statistique sur
le rapport longueur / largeur avec un rectangle considéré comme harmonieux par
les élèves, il ressort que pour les élèves ce rapport doit être proche de 2.
Dans un deuxième temps il a été
procédé à la détermination de la valeur exacte du nombre
. Puis un travail sur le puzzle de Lewis-Carol a permis de
retrouver le nombre d’or dans une configuration transformant un carré en rectangle.
 Les élèves ont également observé
la convergence du quotient entre deux termes consécutifs des suites de Fibonacci vers le nombre d'or
Les élèves ont également observé
la convergence du quotient entre deux termes consécutifs des suites de Fibonacci vers le nombre d'or
Lors de la dernière séquence, les
élèves ont effectué une recherche libre sur des situations où l’on peut penser
retrouver un lien avec le nombre d’or et de restituer leur recherche sur un
document dactylographié. Une sélection
du travail rendu est disponible sur le site
Pierre Rolland
BORDALO Diane
seconde 7
Le nombre d’or
Dans quelles situations se trouve le nombre Phi ?
1ère situation :
La pyramide de Khéops
Les 3 pyramides
égyptiennes de Gizeh ont été les dernières demeures des pharaons Kheops,
Khephren et Mykérinos. Elles ont été construites vers 2600 avant JC. La plus grande d'entre elles fut
construite pour recevoir le corps du souverain Kheops et mesure 146,60 mètres
de haut et 231 mètres de côté. Elle est l'une des sept merveilles du monde.
Khephren, Khéops, Mykérinos
Présentation de la
pyramide :
La pyramide est à base
carrée et ses dimensions originales sont de 146,60 mètres (à un cm près) de
hauteur, 231 mètre de côté (à 1 mètre près).
Hauteur de la face
mesurée sur le plan incliné = 186 m
Périmètre 922 m
Surface 53 056 m²
Volume : évalué à 2 592 341
m³ (ou 2 521 000 m³) à l'origine ; aujourd'hui : 2 352 000 m³
Masse 5 000 000 t
Calcul de la pyramide :
SH représente la hauteur de la pyramide de longueur h = 146,60
SH représente la hauteur de la pyramide de longueur h = 146,60
La pyramide est à base
carrée et ses dimensions originales sont de 146,60 mètres (à un cm près) de
hauteur, 231 mètre de côté (à 1 mètre près).
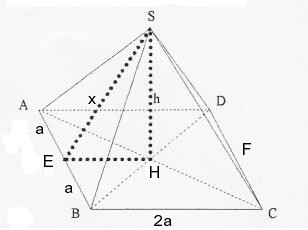
On a schématisé ci-dessus la pyramide de Kheops.
SH représente la hauteur de la pyramide de
longueur h = 146,60 m
AB représente un côté de la pyramide, de
longueur 2a = 231 m
Soit E le milieu de ce côté. On a alors :
AE = EB = EH = a
On pose : SE = SE est appelé l’apothème de la
pyramide.
Le triangle SHE ainsi obtenu est un triangle rectangle en
H. D’après le théorème de Pythagore, on a :
x² = a² + h²
x² = (231/2)² + 146,60²
x² =186,63 m (à 1 cm près)
=186,63 m (à 1 cm près)
Et on a : a = 186,63/231/2 = 1,616 (à un millième près)
Ainsi, le rapport de l’apothème sur une demi-base est
bien égal au nombre phi (aux incertitudes de mesures près) !!
Fléty Amélie seconde 7
MPS : Où se
cache le nombre d’or ?
Situation n°1
Thème 1 : L’architecture
a)
Démonstration par calculs
Nous pouvons remarquer que trois nombres sont apparents sur
la photographie : 21, 34 et 55 et ils ne sont pas là au hasard. Ils font
partis de la suite de Léonardo Fibonacci dont les nombres s’additionnent hormis
les deux premiers puis se divisent avec le résultat toujours au numérateur et
le précédent au dénominateur. C’est la suite qui se rapproche le mieux du
nombre d’or avec des quotients juste supérieur ou inférieur au nombre d’or. Je
prends les deux nombres 1 et 1 de la suite puis je poursuis des additions et
des divisions :
|
Termes
de la suite
|
Quotients
|
|
1
|
/
|
|
1
|
/
|
|
1 +1 = 2
|
2/1 = 2
|
|
2 + 1 = 3
|
3/2 =
1,5
|
|
2 + 3 = 5
|
5/3 est
environ égal à 1,667
|
|
3 + 5 = 8
|
8/5 =
1,6
|
|
5 + 8 = 13
|
13/8 =
1,625
|
|
8 + 13 =
21
|
21/13
est environ égal à 1,615
|
|
13 + 21
= 34
|
34/21
est environ égal à 1,619
|
|
21 + 34
= 55
|
55/34
est environ égal à 1,618
|
|
Etc
|
etc
|
On voit réapparaître nos 3 nombres et leurs quotients se rapprochent
petits à petits au nombre d’or qui est environ égal à 1,618. Donc je peux dire
que la personne à l’origine de la construction de ce théâtre ou plutôt à
l’origine de ces plans à bel et bien utilisé le nombre d’or pour pouvoir avoir
un endroit harmonieux. Tout en essayant de s’y approcher au maximum
Situation n°2
Thème 2 : La
nature
I]
Explications
a)
Démonstration par calcul
·
Dans
un tournesol, on peut voir des spirales qui tournent soit dans le sens des
aiguilles d’une montre ou dans le sens inverse. On remarque que ces spirales
qui tournent dans le sens horaire et dans le sens inverse si on fait la somme
du nombre de spirales dans un sens puis de l’autre, leurs
résultats sont deux chiffres consécutifs de la suite de Fibonacci :
|
Termes
de la suite
|
Quotients
|
|
1
|
/
|
|
1
|
/
|
|
1 +1 = 2
|
2/1 = 2
|
|
2 + 1 =
3
|
3/2 =
1,5
|
|
2 + 3 =
5
|
5/3 est
environ égal à 1,667
|
|
3 + 5 =
8
|
8/5 =
1,6
|
|
5 + 8 =
13
|
13/8 =
1,625
|
|
8 + 13 =
21
|
21/13
est environ égal à 1,615
|
|
13 + 21
= 34
|
34/21
est environ égal à 1,619
|
|
21 + 34
= 55
|
55/34
est environ égal à 1,618
|
|
Etc
|
etc
|
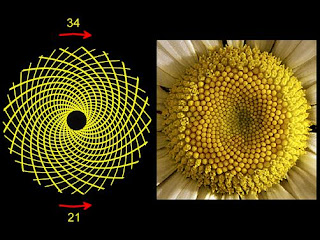
Par
exemple dans le tournesol suivant :
Nous pouvons voir deux nombres consécutifs de la suite de
Fibonacci 21 et 34. Le nombre de spirales dans le sens horaire est plus petit
que le nombre de spirales dans le sens inverse. Suivant la taille du tournesol
les résultats augmentent 34 et 55 par exemple.
Gady Aubin seconde 7
Gady Aubin seconde 7
1 –
Architecture
On retrouve dès l’Antiquité la notion de nombre d’or
en architecture. Le Panthéon, créé par Phidias, aurait des dimensions idéales
sur sa façade. Ces résultats sont contestés et variés, mais il a été néanmoins
prouvé que si on compare les mesures de sa hauteur et de sa longueur, le rapport est environ
égal au nombre d’or. C’est d’ailleurs en l’honneur de Phidias que ce nombre a
été appelé phi, ou Φ.
 Au XXème siècle, des architectes
s’intéressent à ce nombre. Le Corbusier, célèbre architecte, met en place le
Modulor, une représentation idéale permettant de placer l’homme dans un
environnement proche de la nature, puisqu’équivalent ou presque au nombre d’or.
Il le représente dans sa taille idéale,
et propose du mobilier adapté à sa taille. Il s’agit d’une représentation plus
précise de l’homme de Vitruve de Léonard de Vinci. La Cité Radieuse de
Marseille a donc été créée avec ce modèle, pour permettre un
« épanouissement » de l’Homme.
Au XXème siècle, des architectes
s’intéressent à ce nombre. Le Corbusier, célèbre architecte, met en place le
Modulor, une représentation idéale permettant de placer l’homme dans un
environnement proche de la nature, puisqu’équivalent ou presque au nombre d’or.
Il le représente dans sa taille idéale,
et propose du mobilier adapté à sa taille. Il s’agit d’une représentation plus
précise de l’homme de Vitruve de Léonard de Vinci. La Cité Radieuse de
Marseille a donc été créée avec ce modèle, pour permettre un
« épanouissement » de l’Homme.
2 – Nature
 Dans le monde végétal, le nombre d’or est très
présent si on étudie la disposition des feuilles sur la tige de certaines
espèces (phyllotaxie), ou l’implantation des pétales sur les tournesols, par
exemple. L’écorce des ananas, ou des pommes de pins présentent des motifs liés
à la suite de Fibonacci. Sur les pommes de pins, si on compte le nombre
d’écorce implantées en spirale, on obtient 8 dans un sens, et 13 dans l’autre.
Or, ces deux valeurs sont des nombres de la suite de Fibonacci (0, 1, 1, 2, 3,
5, 8, 13), ce qui permet de le
rattacher au nombre d’or. On retrouve cette logique avec les pétales de
tournesols. Ces résultats ont été prouvés par de nombreux scientifiques, et des
modèles informatiques ont pu confirmer la présence du nombre d’or.
Dans le monde végétal, le nombre d’or est très
présent si on étudie la disposition des feuilles sur la tige de certaines
espèces (phyllotaxie), ou l’implantation des pétales sur les tournesols, par
exemple. L’écorce des ananas, ou des pommes de pins présentent des motifs liés
à la suite de Fibonacci. Sur les pommes de pins, si on compte le nombre
d’écorce implantées en spirale, on obtient 8 dans un sens, et 13 dans l’autre.
Or, ces deux valeurs sont des nombres de la suite de Fibonacci (0, 1, 1, 2, 3,
5, 8, 13), ce qui permet de le
rattacher au nombre d’or. On retrouve cette logique avec les pétales de
tournesols. Ces résultats ont été prouvés par de nombreux scientifiques, et des
modèles informatiques ont pu confirmer la présence du nombre d’or.
Dans le règne animal, on retrouve le nombre d’or sur
la spirale du Nautile (ci-contre). Il s’agit en fait d’une spirale logarithmique
qui est composée d’une série de rectangles d’or décroissants. D’ailleurs, si on
étudie la taille de ces rectangles, on retrouve la suite de Fibonacci.
On
trouve également le nombre d’or dans la double spirale de l’ADN. En effet, si
on étudie la taille d’un cycle de double spirale, il mesure 34 angströms par 21, qui sont deux valeurs de la suite
Fibonacci.
3 – Art
 Le nombre d’or est souvent représenté et démontré
dans les tableaux, mais bien souvent à tort. Parfois, l’artiste veut simplement
représenter les proportions de manière harmonieuse, proportions proches du
nombre d’or. On a donc souvent tendance à assimiler des polygones à des
rectangles ou des segments d’or. Seuls quelques artistes, plutôt récents ont
créés leurs œuvres à partir du nombre d’or. Salvador Dali, par exemple, a
travaillé sciemment à partir du nombre d’or, pour s’amuser (Le Sacrement de la
dernière Cène, voir à droite) : la table est exactement à la section
d’or de la hauteur de la peinture. On peut citer aussi Piet Mondrian.
Le nombre d’or est souvent représenté et démontré
dans les tableaux, mais bien souvent à tort. Parfois, l’artiste veut simplement
représenter les proportions de manière harmonieuse, proportions proches du
nombre d’or. On a donc souvent tendance à assimiler des polygones à des
rectangles ou des segments d’or. Seuls quelques artistes, plutôt récents ont
créés leurs œuvres à partir du nombre d’or. Salvador Dali, par exemple, a
travaillé sciemment à partir du nombre d’or, pour s’amuser (Le Sacrement de la
dernière Cène, voir à droite) : la table est exactement à la section
d’or de la hauteur de la peinture. On peut citer aussi Piet Mondrian.
En
musique, le nombre d’or n’a sans doute pas été utilisé consciemment par J-S
Bach dans ses compositions, mais plutôt pour avoir un rendu harmonieux. En
effet, la proportion du temps de l’introduction de certains morceaux par
rapport à la pièce entière est parfois proportionnelle au nombre d’or. Comme
pour la peinture, le nombre d’or a été utilisé par des artistes plus récents
comme Béla Bartók, compositeur.
On
peut aussi retrouver la suite de Fibonacci dans la poésie. Le nombre de pieds
par vers est parfois significatif, même si ces données n’ont sans doute pas été
voulues par l’écrivain. Il s’agit plutôt d’une logique harmonieuse encore une
fois, qui semble-t-il est justifié puisque ce nombre d’or est censé être
harmonieux.
Exemple :
Que j’aime voir, chère
indolente, (8 pieds)
De ton corps si beau
(5 pieds)
Baudelaire
Ø
5/8 : valeurs suivies dans la suite de
Fibonacci






Un travail très intéressant.Bravo à Amélie, Diane et Aubin !
RépondreSupprimer